Dans cette activité nous allons mettre en œuvre la méthode d'Euler qui permet de résoudre numériquement et de manière approchée une équation différentielle du 1er ordre. Nous l'appliquerons à l'exemple du circuit RC série. L'équation différentielle qui pilote ce circuit peut être résolue analytiquement de manière exacte, comme vous le savez. Utiliser la méthode d'Euler sur cet exemple n'est donc pas nécessaire en réalité, mais l'avantage est qu'il s'agit d'un exemple simple dont on connait la solution exacte, ainsi nous pourrons comparer cette dernière avec ce que nous obtiendrons en appliquant l'algorithme d'Euler !
On a \( E=5 \text{ V} \), \( R=1000 \text{ Ω} \) et \(C=100 \text{ nF} \).
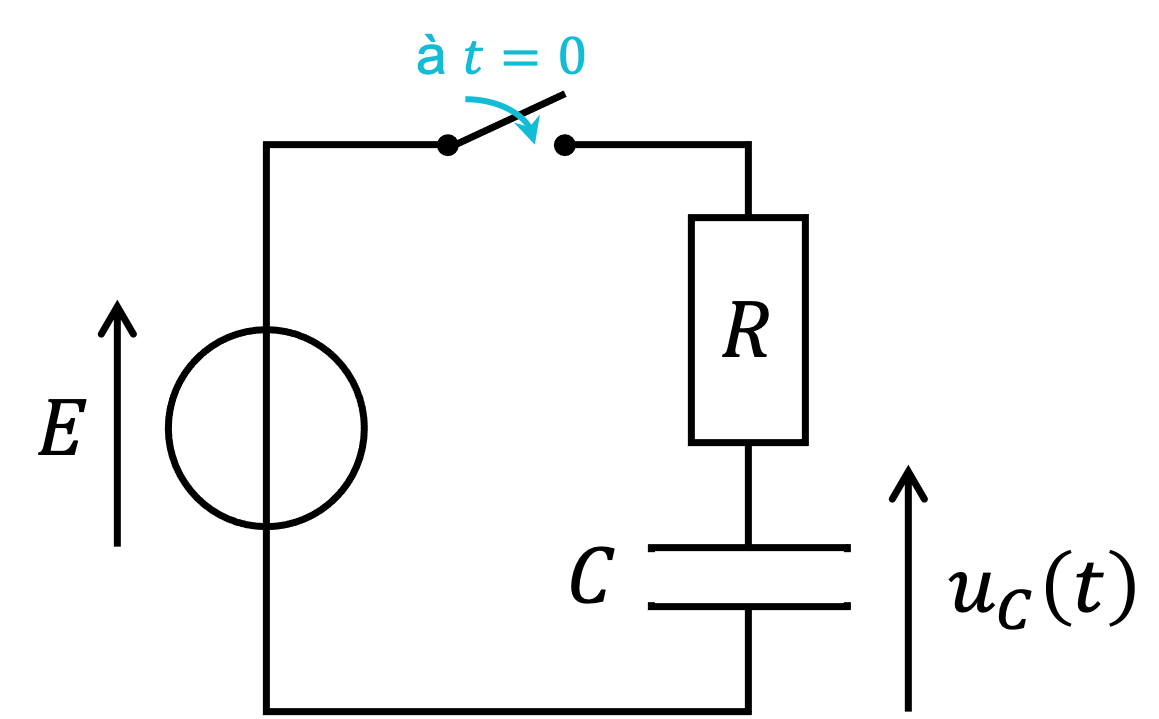
Initialement le condensateur est déchargé, on a donc \( u_c(0^-)=0 \). A l'instant \( t=0 \), on ferme l'interrupteur.
C'est donc cette équation différentielle que nous allons tenter de résoudre numériquement aujourd'hui.
• Définir les constantes nécessaires avec leur valeur dans le Système International d'unités : E, R et C.
• Définir également la durée totale tf sur laquelle on veut résoudre, en fonction de R et C (voir question précédente).
• Définir un nombre N de divisions de cette intervalle de temps pour appliquer la méthode d'Euler (on pourra par exemple choisir \(N=10\) pour commencer).
• Définir alors le pas de calcul dt en fonction de tf et N (ne pas donner de valeur numérique, écrire le calcul en fonction de tf et N, pour pouvoir ajuster les valeurs de tf ou de N facilement dans la suite de l'activité).
Maintenant, nous allons créer des listes (ou plutôt des "tableaux numpy") pour y stocker les valeurs de temps, de tensions et de dérivées.
• Définir un tableau (liste) numpy t contenant les \(N\) instants \(t_i\) régulièrement espacés entre 0 et tf.[Note]
• Définir un tableau numpy Uc contenant pour l'instant \(N\) zéros. On le remplira par la suite : il contiendra les valeurs de la tension \(u_c(t_i)\) aux différents instants \(t_i\) de calcul.[Note]
• Définir un autre tableau numpy dUc_dt contenant lui aussi pour l'instant \(N\) zéros. On le remplira par la suite : il contiendra les valeurs de la dérivée \( \frac{\text{d}u_c}{\text{d}t}(t_i) \) aux différents instants \(t_i\) de calcul[Note].
Pour résoudre numériquement l'équation différentielle, nous utilisons la méthode d'Euler qui approxime la dérivée par :\( \frac{\text{d}f}{\text{d}t} \approx \frac{f(t+\text{d}t) - f(t)}{\text{d}t} \)
• Initialisation : fixer dans Uc[0] la valeur de la condition initiale connue \( u_c(0) \).
• Dans une boucle[Note], on calcule les valeurs suivantes de \( u_c \) de proche en proche :
- calculer dUc_dt[i] en fonction de Uc[i] conformément à l'équation différentielle à résoudre,
- puis calculer Uc[i+1] en fonction de Uc[i] suivant la méthode d'Euler.
Il ne reste plus qu'à tracer le graphe des Uc en ordonnées et des t en abscisses, pour visualiser la solution approchée ainsi obtenue !
Puisque l'équation différentielle sur laquelle on travaille est linéaire, il existe une solution analytique exacte. Il serait donc intéressant de comparer la solution approchée obtenue avec la solution exacte !
• Dans la cellule Python précédente, ajouter une ligne pour calculer UcExacte en fonction de t, E, R et C.[Note]
Puis, dans le même graphe, superposer cette solution exacte en ajoutant la ligne plt.plot(t,UcExacte).
• Exécuter à nouveau le programme en choisissant des nombres d'itérations N différents. Commenter.
