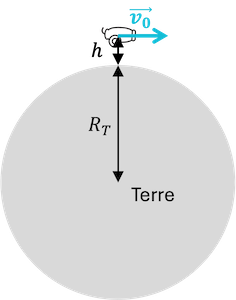
ACTIVITE 4 – Mouvement dans un champ de force centrale gravitationnelle

Chargement de Python... Veuillez patienter.

On souhaite obtenir la trajectoire d'un projectile lancé depuis la Terre, dans le champ gravitationnel de cette dernière. Nous allons considérer un projectile de masse \(m\) situé à une distance initiale \(r_0=R_T+h\) du centre de la Terre, et envoyé avec une vitesse initiale de norme \(v_0\) dans une direction horizontale (orthogonale à la verticale du lieu), comme sur le schéma ci-contre.

Pour cela, nous allons résoudre numériquement les équations différentielles données par le P.F.D., qui sont couplées et non linéaires.

On se place dans le référentiel géocentrique, supposé galiléen, et associé à deux axes orthonormés \((Ox)\) et \((Oy)\) d'origine \(O\) au centre de la Terre.

I - Obtention des équations différentielles du mouvement

Comme on sait d'après le cours que le mouvement est plan (conservation du moment cinétique), plaçons-nous d'abord en coordonnées polaires, puisque la force gravitationnelle s'écrira naturellement dans cette base.

Ecrire (à un instant quelconque au cours du mouvement) l'expression de la force gravitationnelle \(\overrightarrow{F_g}\) que ressent le projectile de masse \(m\) de la part de la Terre de masse \(M_T\), en fonction de la constante de gravitation universelle \(G\), de la distance \(r\) au centre de la Terre (coordonnée polaire) et du vecteur unitaire \(\overrightarrow{u_r}\) des coordonnées polaires.[Note]
\overrightarrow{F_g}=\left(\right)\overrightarrow{u_r}

Nous allons maintenant passer aux coordonnées cartésiennes, puisque cela nous permettra de tracer directement la trajectoire avec matplotlib.

Réécrire la force en coordonnées cartésiennes, c'est-à-dire en fonction des coordonnées \(x\) et \(y\) et des vecteurs de base \(\overrightarrow{u_x}\) et \(\overrightarrow{u_y}\). Aide : on exprimera d'une part la distance \(r\) en fonction de \(x\) et \(y\), et on utilisera le fait que \(\overrightarrow{u_r}=\frac{\overrightarrow{OM}}{OM}=\frac{\overrightarrow{OM}}{r}\).[Note]
\overrightarrow{F_g}=\left(\right)\overrightarrow{u_x}+\left(\right)\overrightarrow{u_y}
Après avoir appliqué le P.F.D., en déduire le système de deux équations différentielles couplées dont sont solutions les fonctions \(x(t)\) et \(y(t)\) :
\frac{d^2x}{dt^2}...
\frac{d^2y}{dt^2}...

Nous allons donc résoudre ce système d'équations différentielles couplées et non linéaires, avec solve_ivp() que nous avons déjà rencontrée sur un exemple plus simple lors de l'ACTIVITE 3.

II - Résolution numérique des équations différentielles du mouvement

Comme d'habitude, on commence par importer les bibliothèques dont on aura besoin. Puis on définit les valeurs des paramètres physiques du problème (à compléter) :

Utiliser les équations du P.F.D. obtenues plus haut pour définir les équations différentielles à résoudre, c'est-à-dire \(\ddot{x}\) et \(\ddot{y}\) en fonction de \(x\) et \(y\) :

Pour travailler avec des ordres de grandeurs pertinents pour la durée du mouvement et pour la vitesse initiale, nous allons nous appuyer sur des valeurs obtenues par résolution mathématique exacte dans le cas du mouvement circulaire uniforme.

Rappeler l'expression de la vitesse (qui est constante) sur une orbite circulaire de rayon \(r_0\) :
v_{circ}=
En déduire l'expression de la période de révolution \(T\) sur cette orbite, en fonction du rayon \(r_0\) et de la vitesse constante \(v_{circ}\) sur cette orbite :
T=

Définir cette vitesse de référence vcirc et cette durée de référence T dans le programme (ces valeurs nous serviront ensuite à choisir facilement la vitesse initiale v0 et la durée de résolution tf en rapport à ces valeurs de référence) :

Utilisons maintenant solve_ivp() pour résoudre le système d'équations différentielles equadiffs. Rappelons le mode d'emploi de cette fonction :

solution = sci.solve_ivp(systeme, [t0,tf], [C1,C2,C3,C4], t_eval=liste_t)

    En entrée :
  • systeme est le système différentiel à résoudre, dans notre cas présent c'est equadiffs qui contient dans cet ordre : \(x\), \(\dot{x}\), \(y\), \(\dot{y}\)
  • [t0,tf] est l'intervalle de résolution
  • [C1,C2,C3,C4] est le jeu des conditions initiales, donc dans notre cas ce sont les valeurs (dans cet ordre) de \(x(0)\), \(\dot{x}(0)\), \(y(0)\), \(\dot{y}(0)\)
  • liste_t est la liste des instants où on fait le calcul.

    En sortie :
  • solution.t retournera la liste des instants de calcul (donc identique à liste_t)
  • solution.y[0] retournera les valeurs calculées de la première fonction inconnue, donc dans notre cas les valeurs de \(x(t)\)
  • solution.y[1] retournera les valeurs calculées de la deuxième fonction inconnue, donc dans notre cas les valeurs de \(\dot{x}(t)\)
  • solution.y[2] retournera les valeurs calculées de la troisième fonction inconnue, donc dans notre cas les valeurs de \(y(t)\)
  • solution.y[3] retournera les valeurs calculées de la quatrième fonction inconnue, donc dans notre cas les valeurs de \(\dot{y}(t)\)

Compléter cette instruction avec les quatre valeurs de conditions initiales que nous avons déjà définies précédemment :

Il ne nous reste plus qu'à afficher la trajectoire ! On dessine aussi la Terre, et on repère le point de départ avec une petite marque rouge :

Tracer plusieurs trajectoires différentes en modifiant la valeur de la vitesse initiale v0.
Vous pourrez (par exemple) tracer les trajectoires pour : \[v_0=0,5\times v_{circ}\] \[v_0=0,8\times v_{circ}\] \[v_0=v_{circ}\] \[v_0=1,2\times v_{circ}\] \[v_0=1,3\times v_{circ}\] \[v_0=\sqrt{2}\times v_{circ}\] \[v_0=2\times v_{circ}\]
Il faudra peut-être parfois aussi adapter la durée tf sur laquelle on calcule la trajectoire.

Quelles sont les deux types de trajectoires (courbes géométriques) que l'on obtient ?
Que se passe-t-il en réalité quand \(v_0\lessdot v_{circ}\) ?
Que constate-t-on quand \(v_{circ} \lt v_0 \lt \sqrt{2}\times v_{circ}\) ? Est-ce conforme au cours ?
Que constate-t-on quand \(v_0 \gt \sqrt{2}\times v_{circ}\) ? Est-ce conforme au cours ?
terminal = false packages = ["numpy", "matplotlib", "scipy"] [[fetch]] files = [] import sys import io import traceback from js import document, console, window from pyodide.ffi import create_proxy import base64 # Configuration matplotlib pour PyScript import matplotlib matplotlib.use('Agg') # Backend non-interactif pour PyScript import matplotlib.pyplot as plt # Contexte global partagé entre toutes les cellules global_context = {'plt': plt, 'matplotlib': matplotlib} def capture_output(func, *args, **kwargs): """Capture la sortie d'une fonction""" old_stdout = sys.stdout old_stderr = sys.stderr stdout_capture = io.StringIO() stderr_capture = io.StringIO() sys.stdout = stdout_capture sys.stderr = stderr_capture try: result = func(*args, **kwargs) stdout_output = stdout_capture.getvalue() stderr_output = stderr_capture.getvalue() return result, stdout_output, stderr_output finally: sys.stdout = old_stdout sys.stderr = old_stderr def handle_matplotlib_figures(output_element): """Gère l'affichage des figures matplotlib""" current_figures = plt.get_fignums() if current_figures: # Créer ou récupérer le conteneur des figures figures_container = output_element.querySelector('.figures-container') if not figures_container: figures_container = document.createElement('div') figures_container.className = 'figures-container' figures_container.style.cssText = ''' display: flex; flex-wrap: wrap; gap: 15px; margin: 10px 0; justify-content: center; ''' output_element.appendChild(figures_container) for fig_num in current_figures: fig = plt.figure(fig_num) # Convertir la figure en image base64 buf = io.BytesIO() fig.savefig(buf, format='png', bbox_inches='tight', dpi=150) buf.seek(0) img_data = base64.b64encode(buf.read()).decode() buf.close() # Créer un conteneur pour la figure avec bouton de suppression figure_wrapper = document.createElement('div') figure_wrapper.className = 'figure-wrapper' figure_wrapper.style.cssText = ''' position: relative; display: inline-block; border: 1px solid #ddd; border-radius: 8px; padding: 10px; background: white; box-shadow: 0 2px 5px rgba(0,0,0,0.1); margin: 5px; ''' # Créer l'élément img pour afficher la figure img_element = document.createElement('img') img_element.src = f'data:image/png;base64,{img_data}' img_element.className = 'matplotlib-figure' img_element.style.cssText = ''' max-width: 300px; max-height: 250px; height: auto; display: block; border-radius: 4px; ''' # Créer le bouton de suppression delete_btn = document.createElement('button') delete_btn.innerHTML = '×' delete_btn.className = 'figure-delete-btn' delete_btn.style.cssText = ''' position: absolute; top: 5px; right: 5px; width: 25px; height: 25px; border: none; border-radius: 50%; background: rgba(220, 53, 69, 0.8); color: white; font-size: 16px; font-weight: bold; cursor: pointer; display: flex; align-items: center; justify-content: center; line-height: 1; z-index: 10; ''' delete_btn.title = 'Supprimer cette figure' # Ajouter l'événement de suppression def create_delete_handler(wrapper): def delete_figure(event): wrapper.remove() return delete_figure delete_btn.onclick = create_delete_handler(figure_wrapper) # Assembler la figure figure_wrapper.appendChild(img_element) figure_wrapper.appendChild(delete_btn) figures_container.appendChild(figure_wrapper) # Fermer toutes les figures pour éviter les accumulations plt.close('all') return True return False def execute_python_code(code, cell_id): """Exécute le code Python et affiche le résultat""" output_element = document.querySelector(f'#output-{cell_id}') loading_element = document.querySelector(f'#loading-{cell_id}') # Afficher le loading loading_element.style.display = 'block' # Vérifier s'il y a déjà des figures figures_container = output_element.querySelector('.figures-container') if figures_container: # S'il y a des figures, effacer seulement le contenu texte text_outputs = output_element.querySelectorAll('.text-output') for text_output in text_outputs: text_output.remove() # Réinitialiser le style de base sans effacer les figures output_element.className = 'output' # Vider seulement le texte direct, pas les éléments enfants nodes_to_remove = [] for node in output_element.childNodes: if node.nodeType == 3: # Text node nodes_to_remove.append(node) for node in nodes_to_remove: node.remove() else: # Pas de figures, effacer tout output_element.innerHTML = '' output_element.className = 'output' try: def run_code(): # Exécuter le code dans le contexte global exec(code, global_context) # Si la dernière ligne est une expression (pas un statement), l'évaluer et retourner le résultat lines = code.strip().split('\n') if lines: last_line = lines[-1].strip() # Vérifier que ce n'est pas un statement Python commun if (last_line and not last_line.startswith((' ', '\t')) and not last_line.endswith(':') and not last_line.startswith(('print(', 'import ', 'from ', 'def ', 'class ', 'if ', 'for ', 'while ', 'try:', 'except', 'with ', 'assert ', 'del ', 'pass', 'break', 'continue', 'return', 'yield', 'raise', 'global ', 'nonlocal ', 'plt.', 'fig')) and '=' not in last_line.split('#')[0]): # Éviter les assignments try: return eval(last_line, global_context) except: pass return None result, stdout_output, stderr_output = capture_output(run_code) # Gérer l'affichage des figures matplotlib (s'ajoute aux existantes) has_figures = handle_matplotlib_figures(output_element) # Construire la sortie texte output = "" if stdout_output: output += stdout_output if stderr_output: output += stderr_output if result is not None: output += str(result) if output: # S'il y a déjà des figures, ajouter le texte à la suite if has_figures: text_div = document.createElement('div') text_div.className = 'text-output' text_div.textContent = output output_element.appendChild(text_div) else: output_element.textContent = output elif not has_figures: output_element.textContent = "✓ Code exécuté avec succès" output_element.className = 'output success' except Exception as e: error_output = f"❌ Erreur:\n{str(e)}\n\n{traceback.format_exc()}" output_element.textContent = error_output output_element.className = 'output error' finally: loading_element.style.display = 'none' # Exposer les fonctions à JavaScript window.execute_python_code = create_proxy(execute_python_code) # Signaler que PyScript est prêt console.log("PyScript ready!") try: # Activer l'interface immédiatement status_element = document.querySelector('#pyscript-status') if status_element: status_element.innerHTML = 'Python est prêt ! Vous pouvez maintenant exécuter votre code.' status_element.className = 'pyscript-status pyscript-ready' # Activer tous les boutons d'exécution run_buttons = document.querySelectorAll('.btn-run') for button in run_buttons: button.disabled = False # Notifier JavaScript window.pyScriptIsReady = True except Exception as e: console.log(f"Error during PyScript initialization: {e}")