I - Principe de la méthode dichotomique
On souhaite déterminer une valeur numérique de \(\sqrt{2}\) avec une précision de 5 chiffres après la virgule, en utilisant l'algorithme de dichotomie
C'est cette équation que nous allons chercher à résoudre par dichotomie.
Pour que cette méthode fonctionne, il faut déterminer un intervalle dans lequel cette fonction s'annule une fois et une seule, qui sera notre intervalle de départ. Pour cela, le plus simple est de tracer la courbe représentative de la fonction sur un intervalle "au feeling" (vous avez une idée de la valeur approximative de \(\sqrt{2}\), j'espère...).
Nous avons maintenant une idée de l'intervalle sur lequel chercher la solution.
Ecrire l'algorithme de dichotomie permettant d'obtenir la valeur de \(\sqrt{2}\) à \(10^{-5}\) près.
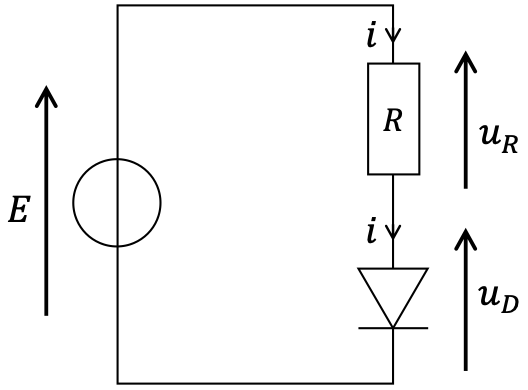
- Passons à un exemple physique concret. Dans ce circuit :
- \( E=5 \text{ V} \)
- \( R = 1,0~\text{k}\Omega \)
- la relation courant-tension de la diode est \( i = I_s\times \left( \mathrm{e}^{u_D/V_0} -1 \right) \)
avec \(I_s=1,0\cdot 10^{-12}\text{ A}\) et \(V_0=26\cdot 10^{-12}\text{ mV}\)
Pour résoudre cette équation par dichotomie, il faudrait déjà avoir une idée approximative de l'intervalle \(\left[u_{D1},u_{D2}\right]\) dans lequel cette fonction s'annule. Pour cela, tracer le graphe de cette fonction et en déduire un intervalle \(\left[u_{D1},u_{D2}\right]\) de départ pour appliquer la dichotomie ensuite.
II - Utilisation de la fonction bisect()
Il existe une fonction bisect() toute prête, disponible dans la bibliothèque scipy.optimize, qui applique automatiquement la méthode dichotomique pour trouver le zéro d'une fonction.
Au lieu de programmer la boucle nous-même, on peut utiliser cette fonction qui fait tout le travail !
Cherchons la documentation de cette fonction sur le site officiel de SciPy :
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.bisect.html
- Points importants à avoir en tête :
- Toujours définir la fonction dont on cherche le zéro avant d'appeler
bisect() - Choisir un bon intervalle de départ : le graphique aide ! → Il faut que f s’annule 1 fois et 1 seule sur cet intervalle.
- bisect() fait ensuite tout le travail : pas besoin de boucle !
Utiliser cette fonction bisect() pour déterminer une valeur numérique de \(\sqrt{2}\), puis pour déterminer le point de fonctionnement du circuit précédent.
