I - La fonction solve_ivp
Nous reprenons la résolution numérique d'équations différentielles, étudiée lors de la séance précédente. Nous avons utilisé la méthode d'Euler, que nous avons codé nous-même en Python. En fait, il existe une fonction solve_ivp déjà implémentée dans la bibliothèque scipy qui permet de résoudre numériquement des équations différentielles (mais toujours d'ordre 1 seulement !), avec un algorithme plus performant que celui d'Euler.
Pour s'entraîner à l'utiliser sur un exemple simple, reprendre le cas du circuit RC série de la séance précédente, et résoudre numériquement l'équation différentielle avec solve_ivp pour déterminer la tension \(u_C(t)\) aux bornes du condensateur entre \(t=0\) et \(t=5RC\).
II - Pendule simple aux grands angles
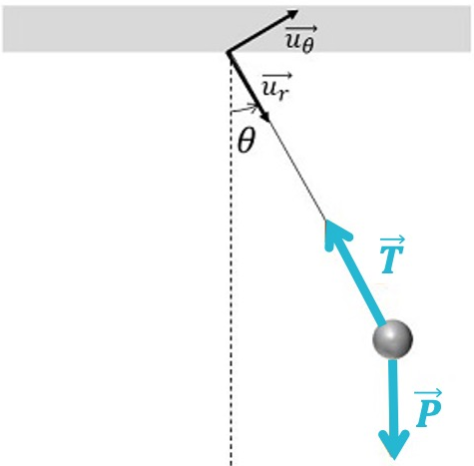
Cette fois-ci, nous allons nous intéresser à un système physique régit par une équation différentielle qui n'admet pas de solution analytique : le pendule simple.
Les conditions initiales seront les suivantes : \[ \begin{Bmatrix} \theta(0)=\theta_0 \\ \dot{\theta}(0)=0 \end{Bmatrix} \]L'angle initial \(\theta_0\) ne sera pas nécessairement petit devant 1 radian.
La longueur du fil sera de \(L=20\text{ cm}\). La pesanteur vaut \(g=9,8\text{ m.s}^{-2}\). On pourra poser \(\omega_0=\sqrt{\frac{g}{L}}\).
En vous aidant de l'énoncé papier, utiliser solve_ivp pour résoudre numériquement cette équation différentielle entre \(t=0\) et \(t=6\times\frac{2\pi}{\omega_0}\).
On pourra tester plusieurs valeurs d'angles initial \(\theta_0\), éventuellement très proches de \(\pi\) comme par exemple : \(\theta_0 = 0.5\pi\) ; \(0.8\pi\) ; \(0.9\pi\) ; \(0.99\pi\)...
Est-ce encore le cas quand on n'est plus aux "petits angles" ? Pour le savoir, nous allons superposer les courbes de \(\theta(t)\) sur le même graphe, pour 10 valeurs différentes d'angle initial \(\theta_0\) échelonnées entre \(0\) et \(\pi\).
Quelques conseils pour vous aider :
- Faire un copier-coller de la cellule précédente dans la cellule vide ci-dessous.
- Remplacer la valeur unique la condition initiale
theta0par un tableau numpy contenant 10 valeurs de conditions initiales échelonnées entre \(0\) et \(\pi\).[Note] - Insérer l'instruction
solution = solve_ivp()dans une boucle, en l'adaptant. - Déplacer l'instruction
plt.plot()à l'intérieur de cette boucle, pour qu'une nouvelle courbe s'affiche à chaque valeur de \(\theta_0\).
fig,ax=plt.subplots() (qui crée la nouvelle zone de graphique) doit être située avant les plt.plot(). La déplacer au début du programme.
Pour mieux voir, on pourra tracer sur une durée entre \(t=0\) et \(t_f=3\frac{2\pi}{\omega_0}\), au lieu de \(t_f=6\frac{2\pi}{\omega_0}\) précédemment.
