 |  dimanche 05 mai 2024 dimanche 05 mai 2024Commencé à 19:05 Terminé à ......... |
EXERCICE 1 : Circuit RC série soumis à un échelon de tension
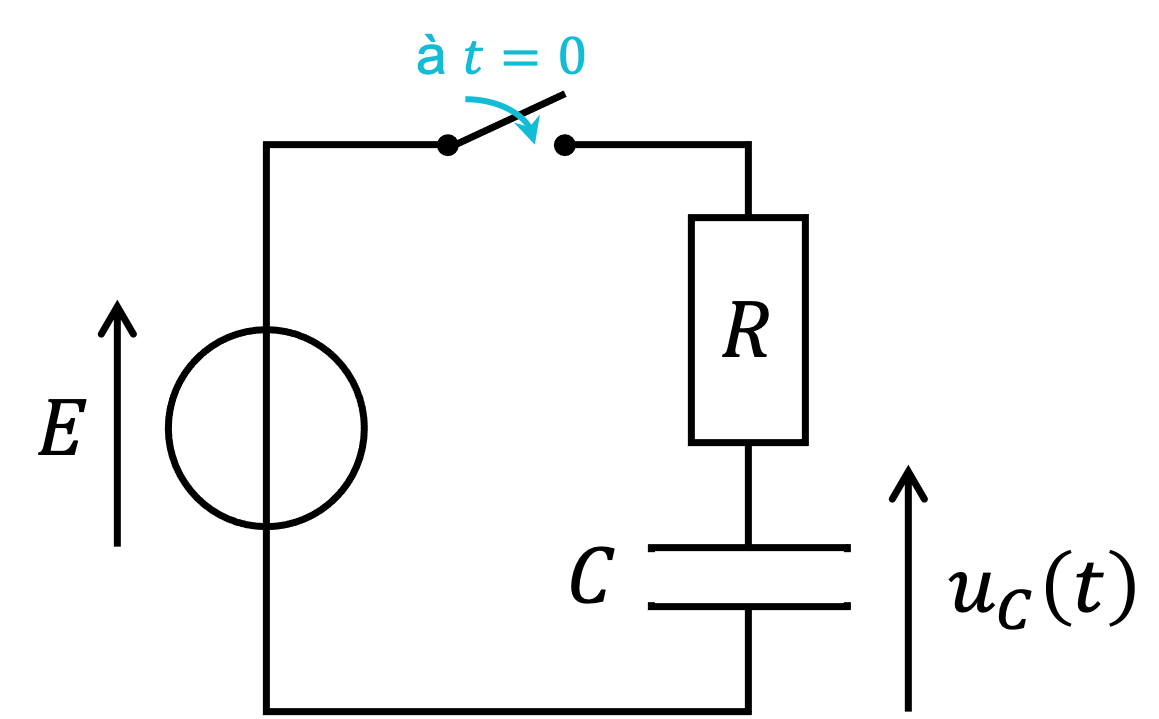
On a \( E=5 \text{ V} \), \( R=1000 \text{ Ω} \) et \(C=100 \text{ nF} \).
Initialement le condensateur est déchargé, on a donc \( u_C(0^-)=0 \). A l'instant \( t=0 \), on ferme l'interrupteur.
1Quelle est l'équation différentielle vérifiée par la tension \( u_C \) à partir de cet instant ?
2Que vaut la tension \(u_C(0)\) aux bornes du condensateur juste après avoir fermé l'interrupteur ? Pourquoi ?
3Au bout de combien de temps environ le régime permanent sera atteint (en fonction des paramètres du problème) ?
Nous allons résoudre numériquement cette équation, en utilisant la méthode d'Euler.
On commence par importer les bibliothèques nécessaires (penser à exécuter le code de chaque cellule en cliquant sur le bouton en bas à droite !) :
4• Définir les constantes nécessaires avec leur valeur dans le Système International d'unités : E, R et C.
• Définir également la durée totale tf sur laquelle on veut résoudre, en fonction de R et C (voir question 3).
• Définir un nombre N de divisions de cette intervalle de temps pour appliquer la méthode d'Euler (on pourra par exemple choisir \(N=10\) pour commencer).
• Définir alors le pas de calul dt en fonction de tf et N (ne pas donner de valeur numérique, écrire le calcul en fonction de tf et N, pour pouvoir ajuster les valeurs de tf ou de N facilement dans la suite de l'activité).
5• Définir une liste numpy t contenant les \(N\) instants \(t_i\) régulièrement espacés entre 0 et tf.[Note]
• Définir une liste numpy Uc contenant pour l'instant \(N\) zéros. On la remplira par la suite : elle contiendra les valeurs de la tension \(u_C(t_i)\) aux différents instants \(t_i\) de calcul.[Note]
• Définir une deuxième liste numpy dUc_dt contenant elle aussi pour l'instant \(N\) zéros. On la remplira par la suite : elle contiendra les valeurs de la dérivée \( \frac{\text{d}u_C}{\text{d}t}(t_i) \) aux différents instants \(t_i\) de calcul[Note].
6C'est parti, on arrive au coeur de l'algorithme d'Euler !
• Que vaut la dérivée \( \frac{\text{d}u_C}{\text{d}t} \) en fonction de \( u_C \) (voir question 1) ?
\frac{\text{d}u_c}{\text{d}t}=
• Initialisation : fixer dans Uc[0] la valeur de la condition initiale connue \( u_C(0) \).
• Dans une boucle[Note], on calcule les valeurs suivantes de \( u_C \) de proche en proche :
- calculer dUc_dt[i] en fonction de Uc[i] conformément à l'équation différentielle à résoudre,
- puis calculer Uc[i+1] en fonction de Uc[i] suivant la méthode d'Euler.
7Il ne reste plus qu'à tracer le graphe des Uc en ordonnées et des t en abscisses, pour visualiser la solution approchée ainsi obtenue !
8Puisque l'équation différentielle sur laquelle on travaille est en fait linéaire, il existe une solution exacte. Il serait donc intéressant de comparer la solution approchée obtenue avec la solution exacte !
• Quelle est la solution mathématique exacte de cette équation différentielle ?
• Dans la cellule de la question 5, ajouter une ligne pour calculer UcExacte en fonction de t, E, R et C.[Note]
Puis, dans le même graphe, superposer cette solution exacte en ajoutant la ligne plt.plot(t,UcExacte).
• Exécuter à nouveau le programme en choisissant des nombres d'itérations N différents. Commenter.
EXERCICE 2 : Chute d'une goutte de pluie avec frottements quadratiques

Intéressons-nous maintenant un exemple où la résolution numérique a un plus grand intérêt, c'est-à-dire à un problème physique décrit par une équation différentielle qui n'est pas linéaire.
On étudie une goutte de pluie de masse \(m\) qui chute verticalement dans le champ de pesanteur. L'air exerce sur cette goutte des frottements fluides proportionnels au carré de la vitesse : \( \overrightarrow{f}=-\alpha v^2 \overrightarrow{u_x} \).
1Quelle est l'équation différentielle vérifiée par la vitesse \(v(t)\) de la goutte ?
2Il s'agit d'une équation non linéaire, sa résolution analytique est difficile... Notre résolution numérique approchée a donc un intérêt.
Néanmoins, sans résoudre, on peut déterminer la vitesse limite atteinte par la goutte en régime permanent. Quelle est son expression ?
A vous de jouer : vous allez écrire un programme Python utilisant la méthode d'Euler pour résoudre cette équation différentielle et connaître la vitesse de la goutte pendant le régime transitoire.
Avant tout, exécuter cette ligne pour effacer les variables définies à l'exercice précédent :
Comme dans le problème ouvert du TD du chapitre C3, on prendra une grosse goutte de pluie supposée sphérique de rayon \(R=4\text{ mm}\).
Sa masse est donc de \( m = \rho\times\frac{4}{3}\pi R^3 = 2,7\cdot 10^{-4}\text{ kg} \).
Le coefficient de frottement vaut \( \alpha = \frac{1}{2}\rho\pi R^2 C_x = \frac{1}{2}\times 1000 \times 3,14 \times \left(0,004\right)^2 \times 0,5 = 1,3 \cdot 10^{-2}\text{ N.s}^2\text{.m}^{-2} \)
3Ecrire le programme Python.
On appellera g la pesanteur terrestre, alpha le coefficient de frottement, v le tableau numpy des vitesses, et a celui des accélérations.
Pour l'intervalle total de temps tf sur lequel résoudre, vous pourrez estimer au doigt mouillé (avec votre sens physique) la durée au bout de laquelle une goutte de pluie initialement immobile atteint sa vitesse de chute limite. Puis, après avoir tracé le graphe, vous pourrez réajuster cette valeur.
4Afficher le graphe de la vitesse approchée \(v(t)\) obtenue :
5Commenter. (La vitesse limite est elle correcte ? Qu'avez-vous constaté pour certains paramétrages de la discrétisation ?....)
Remarque : La solution exacte, difficile à trouver par le calcul (!) est : \[ v(t) = \sqrt{\frac{mg}{\alpha}} \tanh \left(\frac{gt}{\sqrt{\frac{mg}{\alpha}}}\right) \]
FIN DE LA SEANCE
