| QUESTIONS DE COURS DE CETTE SEMAINE |
Q1
|
Quand la lumière se comporte comme des particules…
– Décrire l’expérience de l’effet photoélectrique. Quel aspect en particulier de cette expérience a nécessité d’introduire la notion de photon ? Expliquer pourquoi.
– Donner les relations de Planck-Einstein (énergie, et quantité de mouvement d’un photon). |
Q2
|
Quand les particules matérielles se comportent comme des ondes…
– Dire tout ce que vous savez sur l’expérience d’interférences (fentes d’Young) avec particules matérielles. Puis discussion avec l’interrogateur.
– Donner la relation de De Broglie. |
Q3
|
Définir la fonction d’onde
![Rendered by QuickLaTeX.com \[\psi(x,t)\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-db95c82831ee68b05dc0c2d584f5c32f_l3.png)
d’une particule quantique (lien avec la probabilité de présence). |
Q4
|
Qu’appelle-t-on « l’énergie de point zéro » en mécanique quantique ?
En utilisant le principe d’indétermination de Heisenberg, déterminer une valeur approchée (OdG) de l’énergie de point zéro d’une particule de masse
![Rendered by QuickLaTeX.com \[m\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-efc06065ceafeb36a3282c2ef626a853_l3.png)
piégée dans un puits rectangulaire infini de largeur
![Rendered by QuickLaTeX.com \[L\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-50dc65b99728ffd8aaf5c1908e90ab40_l3.png)
. |
Q5
|
(Révision chapitre B7)
Déterminer les longueurs d’ondes propres
![Rendered by QuickLaTeX.com \[\lambda_n\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-05481df32ac1f7a83ba3f3aeb7eec0c6_l3.png)
et les fréquences propres
![Rendered by QuickLaTeX.com \[f_n\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-0163264f0b7f06d0705366dd52a83002_l3.png)
des ondes stationnaires sur une corde vibrante de longueur
![Rendered by QuickLaTeX.com \[L\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-50dc65b99728ffd8aaf5c1908e90ab40_l3.png)
fixée à ses deux extrémités (on notera
![Rendered by QuickLaTeX.com \[c\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-eb303fff82fd0eed1840d8198fc1ad0c_l3.png)
la célérité des ondes sur la corde). |
Q6
|
En faisant une analogie avec la corde vibrante, déterminer les niveaux d’énergie discrets d’une particule de masse
![Rendered by QuickLaTeX.com \[m\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-efc06065ceafeb36a3282c2ef626a853_l3.png)
piégée dans un puits rectangulaire infini de largeur
![Rendered by QuickLaTeX.com \[L\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-50dc65b99728ffd8aaf5c1908e90ab40_l3.png)
. |
Q7
|
Énoncer le théorème de l’énergie cinétique :
– sous forme différentielle,
– sous forme intégrale (entre deux positions
![Rendered by QuickLaTeX.com \[A\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-c7cd3c29533840a2fa2d926df252f207_l3.png)
et
![Rendered by QuickLaTeX.com \[B\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-964828b226915d810fb8a89d4341d82f_l3.png)
),
– et sous forme dérivée (appelé aussi « théorème de la puissance cinétique »).
Puis : le démontrer (à partir du PFD). |
Q8
|
Énoncer le théorème de l’énergie mécanique :
– sous forme différentielle,
– sous forme intégrale (entre deux positions
![Rendered by QuickLaTeX.com \[A\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-c7cd3c29533840a2fa2d926df252f207_l3.png)
et
![Rendered by QuickLaTeX.com \[B\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-964828b226915d810fb8a89d4341d82f_l3.png)
),
– et sous forme dérivée (appelé aussi « théorème de la puissance mécanique »).
Puis : le démontrer (à partir du TEC). |
Q9
|
a) Donner la relation entre une force conservative
![Rendered by QuickLaTeX.com \[\overrightarrow{F}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-50639a58ff8631c31108d33bdd597f9f_l3.png)
et l’énergie potentielle
![Rendered by QuickLaTeX.com \[\cal{E}_p\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-cccea44b3d32e99201c2b60a640f5d3d_l3.png)
associée.
b) Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle de pesanteur
![Rendered by QuickLaTeX.com \[\cal{E}_{pp}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-a49186210e1e2bfc274c0a8b8c6a1dcf_l3.png)
associée au poids :
![Rendered by QuickLaTeX.com \[\overrightarrow{P}=-mg\overrightarrow{u_z}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-9e0873eb1cbf54dd42be317ab80ee7f4_l3.png)
|
Q10
|
a) Donner la relation entre une force conservative
![Rendered by QuickLaTeX.com \[\overrightarrow{F}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-50639a58ff8631c31108d33bdd597f9f_l3.png)
et l’énergie potentielle
![Rendered by QuickLaTeX.com \[\cal{E}_p\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-cccea44b3d32e99201c2b60a640f5d3d_l3.png)
associée.
b) Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle élastique
![Rendered by QuickLaTeX.com \[\cal{E}_{pel}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-a296a2639ad8da5b39c3a6e681843b9f_l3.png)
associée à la force de rappel d’un ressort :
![Rendered by QuickLaTeX.com \[\overrightarrow{F_R}=-k\left(x-l_0\right)\overrightarrow{u_x}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-526e94f63e57d77a06ded0e4275f6692_l3.png)
|
Q11
|
a) Donner la relation entre une force conservative
![Rendered by QuickLaTeX.com \[\overrightarrow{F}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-50639a58ff8631c31108d33bdd597f9f_l3.png)
et l’énergie potentielle
![Rendered by QuickLaTeX.com \[\cal{E}_p\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-cccea44b3d32e99201c2b60a640f5d3d_l3.png)
associée.
b) Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle gravitationnelle
![Rendered by QuickLaTeX.com \[\cal{E}_{pg}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-088f046baff84fa01c368451d15bb489_l3.png)
associée à la force gravitationnelle :
![Rendered by QuickLaTeX.com \[\overrightarrow{F_g}=-\cal{G}\frac{m_O m}{r^2}\overrightarrow{u_r}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-6ea1914657dbcd2b933fece8b4d35fc1_l3.png)
|
Q12
|
a) Donner la relation entre une force conservative
![Rendered by QuickLaTeX.com \[\overrightarrow{F}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-50639a58ff8631c31108d33bdd597f9f_l3.png)
et l’énergie potentielle
![Rendered by QuickLaTeX.com \[\cal{E}_p\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-cccea44b3d32e99201c2b60a640f5d3d_l3.png)
associée.
b) Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle électrostatique
![Rendered by QuickLaTeX.com \[\cal{E}_{pe}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-8f80e18387dfb63de8c6a06a31a27b8b_l3.png)
associée à la force électrostatique :
![Rendered by QuickLaTeX.com \[\overrightarrow{F_e}=\frac{1}{4\pi\epsilon_0}\frac{q_O q}{r^2}\overrightarrow{u_r}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-c4d14a1a492637b2bffd7b367b6ccc4c_l3.png)
|
Q13
|
a) Donner la relation entre une force conservative
![Rendered by QuickLaTeX.com \[\overrightarrow{F}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-50639a58ff8631c31108d33bdd597f9f_l3.png)
et l’énergie potentielle
![Rendered by QuickLaTeX.com \[\cal{E}_p\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-cccea44b3d32e99201c2b60a640f5d3d_l3.png)
associée.
b) Application : grâce à cette relation, déterminer l’expression de l’énergie électrostatique
![Rendered by QuickLaTeX.com \[\cal{E}_{pe}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-8f80e18387dfb63de8c6a06a31a27b8b_l3.png)
associée à la force électrostatique (pour un champ électrique uniforme) :
![Rendered by QuickLaTeX.com \[\overrightarrow{F_e}=qE\overrightarrow{u_x}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-6a4865872ea0bbd6f5150048be8e8699_l3.png)
|
Q14
|
On considère un mouvement conservatif à 1 degré de liberté
![Rendered by QuickLaTeX.com \[x\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-9a51c841875cccf737cdaf2a71188fca_l3.png)
.
- Justifier qu’une position d’équilibre correspond à un extremum d’énergie potentielle
![Rendered by QuickLaTeX.com \[\cal{E}_p(x)\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-c73aaa9f178e47218da5019894066066_l3.png)
.
- Puis justifier que cet équilibre est stable si cet extremum est un minimum.
|
Q15
|
Montrer qu’il est possible d’approximer un mouvement au voisinage d’une position d’équilibre stable par un oscillateur harmonique.
Que vaut la pulsation des petites oscillations autour de cet équilibre ? |
Q16
|
Expliquer pourquoi un champ magnétique peut dévier la trajectoire d’une particule chargée mais ne peut pas modifier la norme de sa vitesse (une démonstration est demandée). |
Q17
|
Comment peut-on faire en pratique pour générer un champ électrique
![Rendered by QuickLaTeX.com \[\overrightarrow{E}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-a8f0393d28ac04d91794c11721bb8f74_l3.png)
uniforme ? |
Q18
|
Une particule chargée
![Rendered by QuickLaTeX.com \[q\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-c04ace50e46155c33cc6c9ab9b8d0962_l3.png)
et de masse
![Rendered by QuickLaTeX.com \[m\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-efc06065ceafeb36a3282c2ef626a853_l3.png)
, initialement immobile en
![Rendered by QuickLaTeX.com \[A\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-c7cd3c29533840a2fa2d926df252f207_l3.png)
, est accélérée par une tension (différence de potentiel)
![Rendered by QuickLaTeX.com \[U=V_A-V_B\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-ce25ea94861c5efe07a294b3d5f5baa0_l3.png)
appliquée entre deux plaques
![Rendered by QuickLaTeX.com \[A\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-c7cd3c29533840a2fa2d926df252f207_l3.png)
et
![Rendered by QuickLaTeX.com \[B\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-964828b226915d810fb8a89d4341d82f_l3.png)
. Par un bilan énergétique, déterminer sa vitesse atteinte en
![Rendered by QuickLaTeX.com \[B\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-964828b226915d810fb8a89d4341d82f_l3.png)
. |
Q19
|
Déterminer le rayon de la trajectoire d’une particule chargée dans un champ magnétique uniforme dans le cas où le vecteur-vitesse initial est perpendiculaire au champ magnétique, en admettant que cette trajectoire est circulaire. |
Q20
|
Citer une application concrète (au choix) du mouvement de particules chargées dans un champ électrique, ou magnétique, ou les deux.
Expliquer sommairement le fonctionnement. |
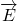 ou
ou 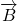 (chapitre C5)
(chapitre C5)![Rendered by QuickLaTeX.com \[\overrightarrow{E}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-a8f0393d28ac04d91794c11721bb8f74_l3.png)
![Rendered by QuickLaTeX.com \[\overrightarrow{B}\]](https://physique-pcsi.prepa-balzac.fr/wp-content/ql-cache/quicklatex.com-b9cf7080084e3ca9069f408c911b64cc_l3.png)
