Du 06/01 au 10/01/2020 – La Physique en PCSI

En cette première semaine de rentrée de l’année 2020, les colles de physiques seront consacrées (en questions de cours et/ou en exercices) :

au filtrage de signaux par des circuits électriques analogiques,
à la physique des ondes (interférences, battements, et ondes stationnaires).

La référence concernant le détail des capacités exigibles sur ces chapitres est, comme toujours, le programme officiel de PCSI. Pour les étudiants, je vous rappelle que vous pouvez retrouver la liste de ces compétences en bas de la première page de chaque chapitre (après la table des matières).
Bonne rentrée à toutes et à tous !

Q1	Donner la configuration du pont diviseur de tension (avec les impédances), et la formule associée. Puis démontrer la formule. Remarque : Inspirez-vous de la démonstration avec les résistances au chapitre B1 : c’est la même.
Q2	Soit un signal périodique $s(t)$ . Donner la définition de la valeur moyenne, et de la valeur efficace. Donner l’expression de la valeur efficace d’un signal périodique quelconque en fonction de la valeur efficace de chacun des harmoniques. Que vaut la valeur efficace d’un signal sinusoïdal $s(t)=S_m \cos(\omega t + \varphi)$ ?
Q3	Sur un exemple au choix, montrer que la fonction de transfert d’un filtre dépend de la présence ou non d’une impédance de charge connectée en sortie.
Q4	Définir l’impédance d’entrée, et l’impédance de sortie d’un quadripôle. Proposer un exemple.
Q5	Rappeler (sans démonstration) la condition à respecter lors d’une mise en cascade de plusieurs filtres les uns à la suite des autres, pour que la fonction de transfert (en sortie ouverte) de l’ensemble soit égale au produit des fonctions de transfert (en sorties ouvertes) de chacun.
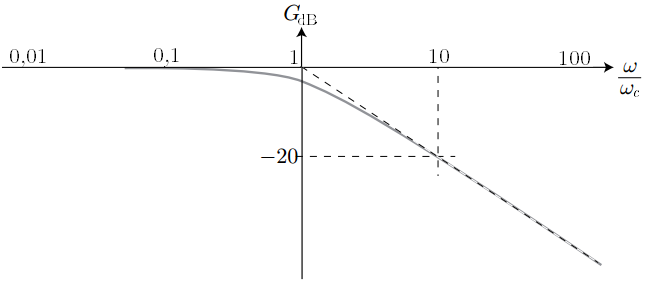
Q6	L’interrogateur vous donne le diagramme de Bode en gain ainsi que la fonction de transfert d’un filtre passe-bas du 1^er ordre : $\underline{H}=H_0\frac{1}{1+j\frac{\omega}{\omega_c}}$ avec ici $H_0 = 1$ . Justifier les pentes des deux asymptotes du diagramme de Bode en gain (à basses et à hautes fréquences).
Q7	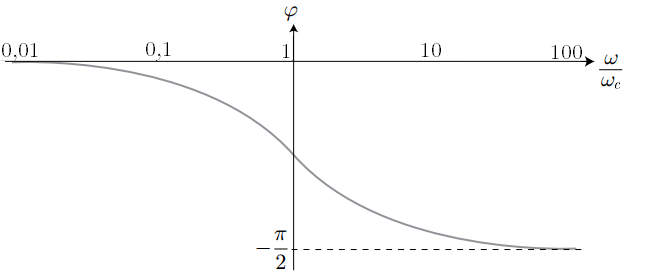L’interrogateur vous donne le diagramme de Bode en phase ainsi que la fonction de transfert d’un filtre passe-bas du 1^er ordre : $\underline{H}=H_0\frac{1}{1+j\frac{\omega}{\omega_c}}$ avec ici $H_0 = 1$ . Justifier valeurs des asymptotes horizontales du diagramme de Bode en phase (à basses et à hautes fréquences).
Q8	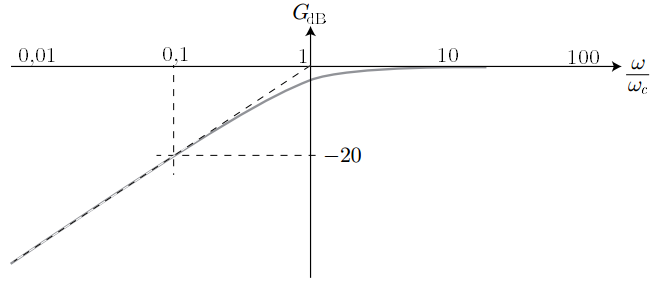L’interrogateur vous donne le diagramme de Bode en gain ainsi que la fonction de transfert d’un filtre passe-haut du 1^er ordre : $\underline{H}=H_0\frac{j\frac{\omega}{\omega_c}}{1+j\frac{\omega}{\omega_c}}$ avec ici $H_0 = 1$ .Justifier les pentes des deux asymptotes du diagramme de Bode en gain (à basses et à hautes fréquences).
Q9	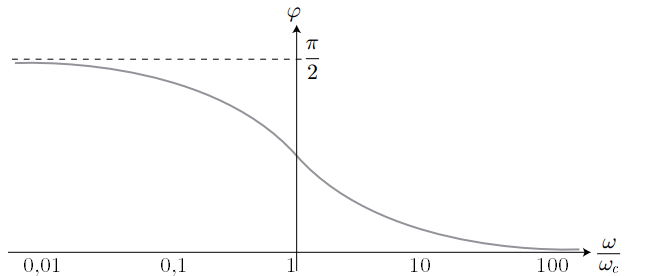L’interrogateur vous donne le diagramme de Bode en phase ainsi que la fonction de transfert d’un filtre passe-haut du 1^er ordre : $\underline{H}=H_0\frac{j\frac{\omega}{\omega_c}}{1+j\frac{\omega}{\omega_c}}$ avec ici $H_0 = 1$ . Justifier valeurs des asymptotes horizontales du diagramme de Bode en phase (à basses et à hautes fréquences).
Q10	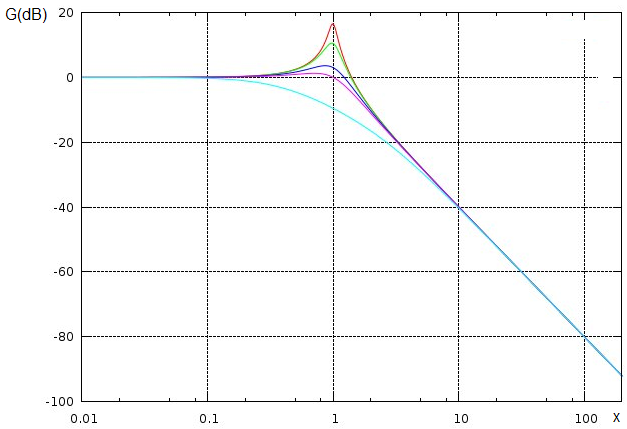L’interrogateur donne la fonction de transfert d’un filtre passe-bas du 2^nd ordre, ainsi que son diagramme de Bode en gain (les différentes couleurs correspondent à différentes valeurs du paramètre $Q$ ) : $\underline{H}=H_0\frac{1}{1-x^2+j\frac{x}{Q}}$ où on a posé $x=\frac{\omega}{\omega_0}$ avec ici $H_0 = 1$ . Justifier les pentes des deux asymptotes (à basses et à hautes fréquences). Expliquer ce qui se passe aux alentours de $x=1$ . Est-ce souhaitable pour un filtre passe-bas ? Comment choisir alors le paramètre $Q$ ?
Q11	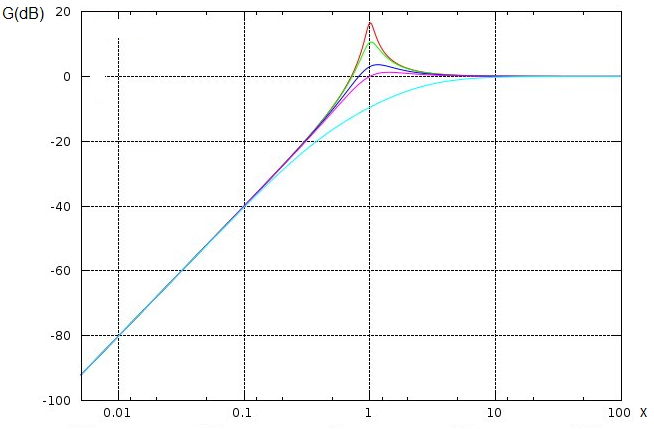L’interrogateur donne la fonction de transfert d’un filtre passe-haut du 2^nd ordre, ainsi que son diagramme de Bode en gain (les différentes couleurs correspondent à différentes valeurs du paramètre $Q$ ) : $\underline{H}=H_0\frac{-x^2}{1-x^2+j\frac{x}{Q}}$ où on a posé $x=\frac{\omega}{\omega_0}$ avec ici $H_0 = 1$ . Justifier les pentes des deux asymptotes (à basses et à hautes fréquences). Expliquer ce qui se passe aux alentours de $x=1$ . Est-ce souhaitable pour un filtre passe-haut ? Comment choisir alors le paramètre $Q$ ? Remarque : nous n’avons pas fait l’exemple du passe-haut du 2nd ordre en cours, mais adaptez les calculs du passe-bas (question précédente), la méthode est la même !
Q12	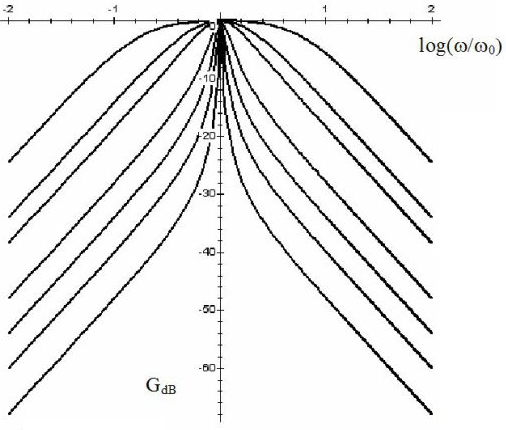L’interrogateur donne la fonction de transfert et le diagramme de Bode en gain d’un filtre passe-bande du 2^nd ordre (les différentes courbes correspondent à différentes valeurs du paramètre $Q$ ) : $\underline{H}=H_0\frac{j\frac{x}{Q}}{1-x^2+j\frac{x}{Q}}$ où on a posé $x=\frac{\omega}{\omega_0}$ avec ici $H_0 = 1$ . Justifier les pentes des asymptotes à basses fréquences et à hautes fréquences. Comment choisir la valeur du paramètre $Q$ pour avoir un filtre très sélectif ?
Q13	Rappeler la définition de la « pulsation de coupure » (en utilisant le gain $G$ , puis le gain en décibels $G_{dB}$ ).
Q14	L’interrogateur fournit : La fonction de transfert d’un passe-bas du 1^er ordre : $\underline{H}=\frac{1}{1+j\frac{\omega}{\omega_c}}$ La fonction de transfert d’un passe-haut du 1^er ordre : $\underline{H}=\frac{j\frac{\omega}{\omega_c}}{1+j\frac{\omega}{\omega_c}}$ Indiquer (en le justifiant) quel type de filtre utiliser et dans quelles conditions pour obtenir un filtre : – dérivateur ; – intégrateur ; – moyenneur.
Q15	Donner les deux écritures possibles d’une onde quelconque se propageant le long d’un axe $(Ox)$ dans le sens des $x$ croissants, puis dans le sens des $x$ décroissants. Même question, mais cette fois-ci dans le cas particulier d’une onde sinusoïdale (en fonction de la pulsation $\omega$ et du nombre d’onde $k$ ). Donner l’expression de la période temporelle $T$ et de la période spatiale $\lambda$ , en fonction de la pulsation ou du nombre d’onde. Quel est le lien entre ces deux périodes ? Le démontrer.
Q16	Qu’appelle-t-on “différence de marche” $\delta$ entre deux ondes, en un point $P$ d’observation ? Quel est le lien entre la différence de marche $\delta$ , et le déphasage $\Delta\varphi$ entre deux ondes sinusoïdales ? Pour quelle(s) valeurs de $\delta$ a-t-on interférences constructives ? interférences destructives ?
Q17	On superpose deux signaux de même amplitude et de fréquences $f_1$ et $f_2$ légèrement différentes. Dessiner l’allure du signal résultant, en fonction du temps. Comment appelle-t-on ce phénomène ? Préciser la période des battements, et la fréquence du signal modulé par ces battements, en fonction des deux fréquences de départ $f_1$ et $f_2$ . (L’interrogateur pourra éventuellement vous demander une démonstration, ou pas…)
Q18	Calculer l’onde résultant de la superposition de deux ondes sinusoïdales de même amplitude et de même pulsation, l’une se propageant dans le sens des $x$ croissants, l’autre dans le sens des $x$ décroissants. Pourquoi n’y a-t-il plus de phénomène de propagation ? Comment appelle-t-on une telle onde ?
Q19	Soit une onde stationnaire sinusoïdale sur une corde vibrante de longueur $L$ . La corde est fixée à ses deux extrémités (en $x=0$ et en $x=L$ ). Montrer *par le calcul* qu’il n’y a que certaines fréquences autorisées sur cette corde. Donner l’expression de ces fréquences, appelées “fréquences propres” (on notera $c$ la célérité des ondes mécaniques sur cette corde). Dessiner l’allure des 3 ou 4 premiers modes de vibration de la corde, et vérifier que la relation entre la longueur d’onde et la longueur $L$ de la corde est bien cohérente avec les résultats trouvés précédemment.

Q1

Q2

Q3

Q4

Q5

Q6

Q7

Q8

Q9

Q10

Q11

Q12

Q13

Q14

Q15

Q16

Q17

Q18

Q19