Du 09/02 au 13/02/2026 – La Physique en PCSI

Cette semaine, les colles porteront sur la dynamique du point en référentiel galiléen : utilisation du Principe Fondamental de la Dynamique.

Certaines questions de cours portent sur l’aspect énergétique, mais ce chapitre n’est pas encore au programme des exercices cette semaine.

Désormais vous ne devez plus écrire des équations non homogènes de manière évidente sans vous en rendre compte. Pensez donc à bien vérifier régulièrement l’homogénéité de vos résultats.

Remarque pour les interrogateurs concernant les questions de cours 10, 11, 12, 13 et 14 : J’ai fait le choix de ne pas introduire dès maintenant l’opérateur gradient (nous le verrons plus tard dans l’année). Ainsi le lien entre une force conservative et l’énergie potentielle dont elle dérive est $dE_p=-\overrightarrow{F_c}\cdot d\overrightarrow{OM}$ .

Q. de cours
Exercice

Énoncer (correctement !…) les trois lois de Newton.

Supposons que le référentiel héliocentrique est galiléen.
Le référentiel géocentrique est-il lui aussi galiléen ?
Et le référentiel terrestre ?
Expliquer.

• Donner l’expression (vectorielle) de la force d’interaction gravitationnelle entre deux corps de masses $m_A$ et $m_B$ .
• Donner l’expression (vectorielle) de la force d’interaction électrostatique entre deux corps de charges électriques $q_A$ et $q_B$ .

Remarque : Soyez précis ! C’est-à-dire :
– Vous écrivez la force exercée par qui, sur qui ? (Autrement dit : qui est le système ? qui est l’extérieur ?)
– Faites un schéma.
– Si vous avez besoin d’utiliser un vecteur unitaire $\overrightarrow{u}$ , définissez-le sur le schéma.)

Quelles sont les deux modélisations couramment adoptées pour décrire les frottements fluides ?

Énoncer les lois de Coulomb du frottement solide.

Exercice de cours : glissement sur plan incliné.
Un palet de masse $m$ est posé sur un support incliné d’un angle $\alpha$ avec l’horizontale. On néglige les frottements de l’air, et on suppose que les frottements solides sur le support vérifient les lois de Coulomb de coefficient $f$ donné.
• Déterminer l’angle $\alpha_l$ à partir duquel le palet glisse.
• Pour $\alpha\ge\alpha_l$ , déterminer l’accélération du palet.

• Définir le travail élémentaire d’une force.
• Définir son travail au cours d’un déplacement fini.
• Définir la puissance d’une force.

C’est quoi « l’énergie » ?…

Je vous propose quelques éléments de réponse pour la question 8, qui reprennent ce que nous avons dit en cours ensemble…
1• Il est difficile de définir ce qu’est l’énergie… Elle ne se manifeste que par ses effets.
2• C’est une certaine quantité qui est constante dans l’Univers (l’Univers = « tout » = le système + le milieu extérieur). Le premier principe de la thermodynamique (que nous verrons en avril), postule que cette grandeur « mystérieuse » existe.
3• Le premier principe dit que l’énergie ne peut pas être créée, et ne peut pas disparaître (elle est constante dans l’Univers). Donc si l’énergie du système diminue, c’est forcément qu’elle est cédée au milieu extérieur ; et si l’énergie du système augmente, c’est donc forcément qu’elle est fournie au système de la part du milieu extérieur, de sorte que globalement, l’énergie totale de l’Univers (= le système + le milieu extérieur) reste constante.
(Relisez l’histoire de la mère du petit enfant turbulent Denis la menace et de ses cubes, qui représentent l’énergie. Le système est la maison, et l’Univers est… l’Univers.)
4• Pour aller plus loin que l’histoire racontée par Feynman : les échanges d’énergie entre le système et le milieu extérieur peuvent se faire :
– soit sous forme de travail $W$ , c’est-à-dire sous l’action de forces mécaniques (c’est ce que nous étudions en ce moment dans cette partie C du cours),
– ou bien sous forme de chaleur $Q$ (nous verrons ça plus tard dans la partie D « Thermodynamique »).
Et on a, de manière évidente :

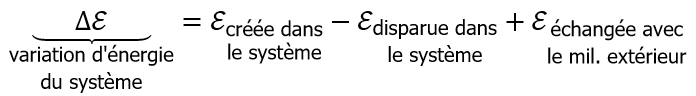
Or le Premier Principe de la thermodynamique postule que (et ça il faut l’admettre, c’est un principe) :

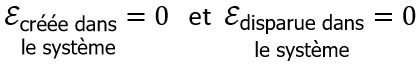
Donc :

Et dans la partie C mécanique du cours, nous n’étudions que les échanges d’énergie sous forme de travail $W$ (pas de notion de « chaleur » $Q$ pour l’instant), donc :

• Énoncer le théorème de l’énergie cinétique :
– sous forme différentielle,
– sous forme intégrale (entre deux positions $A$ et $B$ ),
– et sous forme dérivée (appelé aussi « théorème de la puissance cinétique »).
• Puis : le démontrer (à partir du P.F.D.).

• Donner la relation entre une force conservative $\overrightarrow{F}$ et l’énergie potentielle $E_p$ associée.
• Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle de pesanteur $E_{pp}$ associée au poids : $\overrightarrow{P}=-mg\overrightarrow{u_z}$

• Donner la relation entre une force conservative $\overrightarrow{F}$ et l’énergie potentielle $E_p$ associée.
• Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle de élastique $E_{pe}$ associée à la force de rappel d’un ressort : $\overrightarrow{F_R}=-k\left(x-l_0\right)\overrightarrow{u_x}$

• Donner la relation entre une force conservative $\overrightarrow{F}$ et l’énergie potentielle $E_p$ associée.
• Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle gravitationnelle $E_{pg}$ associée à la force gravitationnelle : $\overrightarrow{F_g}=-G\frac{m_O m}{r^2}\overrightarrow{u_r}$

• Donner la relation entre une force conservative $\overrightarrow{F}$ et l’énergie potentielle $E_p$ associée.
• Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle électrostatique $E_{pel}$ associée à la force électrostatique : $\overrightarrow{F_e}=\frac{1}{4\pi\epsilon_0}\frac{q_O q}{r^2}\overrightarrow{u_r}$

• Donner la relation entre une force conservative $\overrightarrow{F}$ et l’énergie potentielle $E_p$ associée.
• Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle électrostatique $E_{pel}$ associée à la force électrostatique (cas d’un champ électrique uniforme) : $\overrightarrow{F_e}=qE\overrightarrow{u_y}$

Exercice de cours : le pendule simple.
Déterminer l’équation différentielle du mouvement en appliquant le P.F.D. L’approximer dans le cadre des petits angles.
(Evidemment, on fera un schéma, avec l’angle $\theta$ , la base polaire, et les vecteurs-forces).

Exercice de cours : le pendule simple, avec comme conditions initiales $\theta(0)=\theta_0$ et $\dot{\theta}(0)=0$ .
• Déterminer l’équation différentielle du mouvement en appliquant le T.E.C.
• Déterminer l’intégrale première du mouvement.
(Evidemment, on fera un schéma, avec l’angle $\theta$ , la base polaire, et les vecteurs-forces).

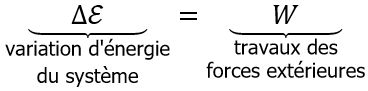
Espace et temps classiques. Référentiel d’observation. Caractère relatif du mouvement.
Description d’un mouvement. Vecteur position, vecteur vitesse, vecteur accélération.
– Savoir établir les expressions des composantes du vecteur position, du vecteur vitesse et du vecteur accélération dans le seul cas des coordonnées cartésiennes et cylindriques.
– Savoir expliquer à partir d’un schéma le déplacement élémentaire dans les différents systèmes de coordonnées, construire la base locale associée et en déduire les composantes du vecteur vitesse en coordonnées cartésiennes et cylindriques.
– Savoir choisir un système de coordonnées adapté au problème posé.
Exemple 1 : mouvement de vecteur accélération constant
– Obtenir la vitesse et la position en fonction du temps. Obtenir la trajectoire en coordonnées cartésiennes.
Exemple 2 : mouvement circulaire uniforme et non uniforme
– Savoir exprimer les composantes du vecteur position, du vecteur vitesse et du vecteur accélération en coordonnées polaires planes.
– Identifier les liens entre les composantes du vecteur accélération, la courbure de la trajectoire, la norme du vecteur vitesse et sa variation temporelle.
– Situer qualitativement la direction du vecteur accélération dans la concavité d’une trajectoire plane.
Forces. Principes des actions réciproques.
– Établir un bilan des forces sur un système, ou plusieurs systèmes en interaction et en rendre compte sur une figure.
Référentiel galiléen. Principe d’inertie.
– Décrire le mouvement relatif de deux référentiels galiléens.
Loi de la quantité de mouvement (“principe fondamental de la dynamique”) dans un référentiel galiléen.
– Déterminer les équations du mouvement d’un point matériel ou du centre d’inertie d’un système fermé.
Mouvement dans un champ de pesanteur uniforme.
– Mettre en équation le mouvement sans frottement et le caractériser comme un mouvement à vecteur-accélération constant.
Influence de la résistance de l’air.
– Prendre en compte la traînée pour modéliser une situation réelle.
– Exploiter une équation différentielle sans la résoudre analytiquement : analyse en ordres de grandeur, détermination de la vitesse limite, utilisation des résultats fournis par un logiciel d’intégration numérique.
Pendule simple.
– Établir l’équation du mouvement du pendule simple.
– Justifier l’analogie avec l’oscillateur harmonique dans le cadre de l’approximation linéaire.
Lois de Coulomb du frottement de glissement dans le cas d’un solide en translation.
– Exploiter les lois de Coulomb fournies dans les trois situations : équilibre, mise en mouvement, freinage.
– Formuler une hypothèse (quant au glissement ou non) et la valider.

Installer comme appli sur le téléphone