Du 09/03 au 13/03/2026 – La Physique en PCSI

Cette semaine de rentrée, les colles de Physique sont consacrées :

à l’aspect énergétique de la mécanique (chapitre C3) ;
au théorème du moment cinétique pour un point matériel (chapitre C6) – la mécanique du solide n’a pas encore été abordée ;
au mouvement dans un champ de forces centrales conservatives (chapitres C7).

Remarques importantes pour les interrogateurs :

J’ai fait le choix de ne pas introduire dès maintenant l’opérateur gradient. Ainsi le lien entre une force conservative et l’énergie potentielle dont elle dérive est 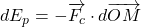$dE_p=-\overrightarrow{F_c}\cdot d\overrightarrow{OM}$ . (Nous verrons la formule $\overrightarrow{F_c}=-\overrightarrow{grad}\left({\cal E}_p\right)$ plus tard dans l’année, au mois de mai.)
Le calcul du moment d’une force par la méthode du bras de levier n’a pas encore été vue. Nous l’aborderons lorsque nous ferons la mécanique du solide.

Questions de cours
Exercice(s)

Soit un mouvement conservatif (c’est-à-dire ${\cal E}_M=cste$ ) à 1 degré de liberté (appelons-le par exemple $x$ , mais ça pourrait aussi être un angle $\theta$ …).

• Expliquer pourquoi l’énergie potentielle ne peut pas dépasser la valeur ${\cal E}_M$ de l’énergie mécanique.
• Comment qualifie-t-on un système qui est « coincé » dans une zone de l’espace ? A l’inverse, que dit-on quand il peut s’éloigner à l’infini ?

Soit un mouvement conservatif (c’est-à-dire ${\cal E}_M=cste$ ) à 1 degré de liberté (appelons-le par exemple $x$ , mais ça pourrait aussi être un angle $\theta$ …).

• Démontrer que les positions d’équilibre correspondent aux extremums du profil d’énergie potentielle ${\cal E}_p(x)$ .
• Démontrer que l’équilibre est stable quand l’énergie potentielle est minimale (et inversement, que l’équilibre est instable quand l’énergie potentielle est maximale).

Soit un mouvement conservatif (c’est-à-dire ${\cal E}_M=cste$ ) à 1 degré de liberté (appelons-le par exemple $x$ , mais ça pourrait aussi être un angle $\theta$ …).

Montrer que l’on peut approximer le mouvement au voisinage d’une position d’équilibre stable par un oscillateur harmonique, et déterminer la pulsation des petites oscillations au voisinage de cet équilibre (en fonction de la masse $m$ de la particule, et de $\frac{d^2{\cal E}_p}{dx^2}\rvert_{x=x_{eq}}$ ).

Exercice de cours : le pendule simple, avec comme conditions initiales $\theta(0)=\theta_0$ et $\dot{\theta}(0)=0$ .
• Déterminer l’équation différentielle du mouvement en appliquant le T.E.M.
• Déterminer l’intégrale première du mouvement.
(Evidemment, on fera un schéma, avec l’angle $\theta$ , la base polaire, et les vecteurs-forces).

Exercice de cours : le pendule simple, avec comme conditions initiales $\theta(0)=\theta_0$ et $\dot{\theta}(0)=0$ .
• Déterminer l’équation différentielle du mouvement en appliquant le T.M.C.
• Déterminer l’intégrale première du mouvement.
(Evidemment, on fera un schéma, avec l’angle $\theta$ , la base polaire, et les vecteurs-forces).

– Qu’appelle-t-on une force centrale ?
– Qu’appelle-t-on une force newtonienne ?
– Donner deux exemples de forces centrales newtoniennes.
– Déterminer l’expression de l’énergie potentielle associée à une force centrale newtonienne, en utilisant la convention habituelle pour la constante.

1. Montrer qu’un point matériel soumis uniquement à une force centrale voit son moment cinétique conservé.
2. En déduire deux conséquences immédiates importantes.

Exprimer la conservation de l’énergie mécanique pour un point matériel soumis uniquement à une force centrale newtonienne, et construire une « énergie potentielle effective » permettant d’étudier uniquement la coordonnée polaire radiale $r(t)$ .
Puis discuter de la nature du mouvement, suivant la valeur de l’énergie mécanique.
On traitera le cas d’une force newtonienne attractive, puis d’une force newtonienne répulsive.

– Déterminer l’expression de la vitesse puis de l’énergie mécanique d’un satellite de masse $m$ en orbite supposée circulaire de rayon $R$ autour d’une planète de masse $m_O$ .
– Sans démonstration, comment généraliser cette expression de l’énergie mécanique au cas où la trajectoire est elliptique (demi-grand axe $a$ , demi-petit axe $b$ ) ?

Déterminer la vitesse $v$ d’un satellite en orbite circulaire de rayon $R$ autour de la Terre. En déduire le rayon $R_{geostat}$ de l’orbite géostationnaire (vous pouvez demander à l’interrogateur les valeurs numériques des constantes dont vous auriez éventuellement besoin pour l’application numérique).

– Définir ce qu’on appelle la « première vitesse cosmique », puis déterminer son expression pour la Terre.
– Rappeler son ordre de grandeur (qui est donc à connaître).

– Définir ce qu’on appelle la « deuxième vitesse cosmique », puis déterminer son expression pour la Terre.
– Rappeler son ordre de grandeur (qui est donc à connaître).

Bien entendu, tous les savoir-faire liés aux chapitres précédents restent exigibles.

ASPECT ENERGETIQUE DE LA DYNAMIQUE

Puissance et travail d’une force.
– Reconnaître le caractère moteur ou résistant d’une force.
– Savoir que la puissance dépend du référentiel.
Loi de l’énergie cinétique et loi de la puissance cinétique dans un référentiel galiléen.
– Utiliser la loi appropriée en fonction du contexte.
Energie potentielle. Energie mécanique.
– Établir et connaître les expressions des énergies potentielles de pesanteur (champ uniforme), énergie potentielle gravitationnelle (champ créé par un astre ponctuel), énergie potentielle élastique, énergie électrostatique (champ uniforme et champ créé par une charge ponctuelle).
Mouvement conservatif.
– Distinguer force conservative et force non conservative. Reconnaître les cas de conservation de l’énergie mécanique. Utiliser les conditions initiales.
– Déduire d’un graphe d’énergie potentielle le comportement qualitatif : trajectoire bornée ou non, mouvement périodique, positions de vitesse nulle.
Positions d’équilibre. Stabilité.
– Déduire d’un graphe d’énergie potentielle l’existence de positions d’équilibre, et la nature stable ou instable de ces positions.
Petits mouvements au voisinage d’une position d’équilibre stable, approximation locale par un puits de potentiel harmonique.
– Identifier cette situation au modèle de l’oscillateur harmonique.
– Utiliser les résultats fournis par une méthode numérique pour mettre en évidence des effets non linéaires

THEOREME DU MOMENT CINETIQUE (EN MECANIQUE DU POINT !)

Moment cinétique d’un point matériel par rapport à un point et par rapport à un axe orienté
– Relier la direction et le sens du vecteur moment cinétique aux caractéristiques du mouvement.
– Maîtriser le caractère algébrique du moment cinétique scalaire.
Moment d’une force par rapport à un point ou un axe orienté
– Calculer le moment d’une force par rapport à un point ou à un axe orienté.
– Théorème du moment cinétique en point fixe dans un référentiel galiléen. Loi scalaire du moment cinétique dans un référentiel galiléen.
– Reconnaître les cas de conservation du moment cinétique.

MOUVEMENT DANS UN CHAMP DE FORCES CENTRALES CONSERVATIVES

Point matériel soumis à un seul champ de force centrale.
– Déduire de la loi du moment cinétique la conservation du moment cinétique.
– Connaître les conséquences de la conservation du moment cinétique : mouvement plan, loi des aires.

Energie potentielle effective. Etat lié et état de diffusion.
– Exprimer la conservation de l’énergie mécanique et construire une énergie potentielle effective.
– Décrire qualitativement le mouvement radial à l’aide de l’énergie potentielle effective. Relier le caractère borné à la valeur de l’énergie mécanique.

Champ newtonien. Lois de Kepler.
– Enoncer les lois de Kepler pour les planètes et les transposer au cas des satellites terrestres.
– Cas particulier du mouvement circulaire : satellite, planète.
– Montrer que le mouvement est uniforme et savoir calculer sa période.
– Etablir la troisième loi de Kepler dans le cas particulier de la trajectoire circulaire. Exploiter sans démonstration sa généralisation au cas d’une trajectoire elliptique.

Satellite géostationnaire.
– Calculer l’altitude du satellite et justifier sa localisation dans le plan équatorial.

Energie mécanique dans le cas du mouvement circulaire puis dans le cas du mouvement elliptique.
– Exprimer l’énergie mécanique pour le mouvement circulaire.
– Exprimer l’énergie mécanique pour le mouvement elliptique en fonction du demi grand axe.

Vitesses cosmiques : vitesses en orbite basse et vitesse de libération
– Exprimer ces vitesses et connaître leur ordre de grandeur en dynamique terrestre.

Installer comme appli sur le téléphone