Du 16/02 au 20/02/2026 – La Physique en PCSI

Cette semaine, les colles porteront sur :

L’aspect énergétique de la mécanique du point matériel ;
Le théorème du moment cinétique (en mécanique du point seulement).

Remarques importantes pour les colleurs :
1. J’ai fait le choix de ne pas introduire dès maintenant l’opérateur gradient (nous le verrons plus tard dans l’année). Ainsi le lien entre une force conservative et l’énergie potentielle dont elle dérive est $dE_p=-\overrightarrow{F_c}\cdot d\overrightarrow{OM}$ .
2. Le TMC est appliqué en mécanique du point pour l’instant (pas de mécanique du solide). Par ailleurs, nous n’avons pas encore vu la notion de bras de levier (j’attends la méanique du solide pour cela).

Questions de cours
Compétences exigibles en exercices

• Définir le travail élémentaire d’une force.
• Définir son travail au cours d’un déplacement fini.
• Définir la puissance d’une force.

C’est quoi « l’énergie » ?…

Je vous propose quelques éléments de réponse pour la question 8, qui reprennent ce que nous avons dit en cours ensemble…
1• Il est difficile de définir ce qu’est l’énergie… Elle ne se manifeste que par ses effets.
2• C’est une certaine quantité qui est constante dans l’Univers (l’Univers = « tout » = le système + le milieu extérieur). Le premier principe de la thermodynamique (que nous verrons en avril), postule que cette grandeur « mystérieuse » existe.
3• Le premier principe dit que l’énergie ne peut pas être créée, et ne peut pas disparaître (elle est constante dans l’Univers). Donc si l’énergie du système diminue, c’est forcément qu’elle est cédée au milieu extérieur ; et si l’énergie du système augmente, c’est donc forcément qu’elle est fournie au système de la part du milieu extérieur, de sorte que globalement, l’énergie totale de l’Univers (= le système + le milieu extérieur) reste constante.
(Relisez l’histoire de la mère du petit enfant turbulent Denis la menace et de ses cubes, qui représentent l’énergie. Le système est la maison, et l’Univers est… l’Univers.)
4• Pour aller plus loin que l’histoire racontée par Feynman : les échanges d’énergie entre le système et le milieu extérieur peuvent se faire :
– soit sous forme de travail $W$ , c’est-à-dire sous l’action de forces mécaniques (c’est ce que nous étudions en ce moment dans cette partie C du cours),
– ou bien sous forme de chaleur $Q$ (nous verrons ça plus tard dans la partie D « Thermodynamique »).
Et on a, de manière évidente :

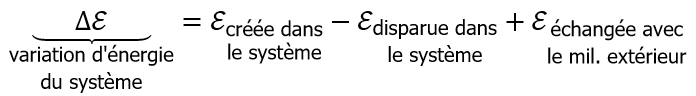
Or le Premier Principe de la thermodynamique postule que (et ça il faut l’admettre, c’est un principe) :

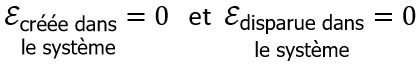
Donc :

Et dans la partie C mécanique du cours, nous n’étudions que les échanges d’énergie sous forme de travail $W$ (pas de notion de « chaleur » $Q$ pour l’instant), donc :

• Énoncer le théorème de l’énergie cinétique :
– sous forme différentielle,
– sous forme intégrale (entre deux positions $A$ et $B$ ),
– et sous forme dérivée (appelé aussi « théorème de la puissance cinétique »).
• Puis : le démontrer (à partir du P.F.D.).

Énoncer le théorème de l’énergie mécanique :
– sous forme différentielle,
– sous forme intégrale (entre deux positions $A$ et $B$ ),
– et sous forme dérivée (appelé aussi « théorème de la puissance mécanique »).
Puis : le démontrer (à partir du T.E.C.).

Énoncer le théorème du moment cinétique par rapport à un point, en précisant les deux hypothèses d’application.
Puis : le démontrer, en précisant à quels endroits de la démonstration vous avez besoin des deux hypothèses.

• Donner la relation entre une force conservative $\overrightarrow{F}$ et l’énergie potentielle $E_p$ associée.
• Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle de pesanteur $E_{pp}$ associée au poids : $\overrightarrow{P}=-mg\overrightarrow{u_z}$

• Donner la relation entre une force conservative $\overrightarrow{F}$ et l’énergie potentielle $E_p$ associée.
• Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle de élastique $E_{pe}$ associée à la force de rappel d’un ressort : $\overrightarrow{F_R}=-k\left(x-l_0\right)\overrightarrow{u_x}$

• Donner la relation entre une force conservative $\overrightarrow{F}$ et l’énergie potentielle $E_p$ associée.
• Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle gravitationnelle $E_{pg}$ associée à la force gravitationnelle : $\overrightarrow{F_g}=-G\frac{m_O m}{r^2}\overrightarrow{u_r}$

• Donner la relation entre une force conservative $\overrightarrow{F}$ et l’énergie potentielle $E_p$ associée.
• Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle électrostatique $E_{pel}$ associée à la force électrostatique : $\overrightarrow{F_e}=\frac{1}{4\pi\epsilon_0}\frac{q_O q}{r^2}\overrightarrow{u_r}$

• Donner la relation entre une force conservative $\overrightarrow{F}$ et l’énergie potentielle $E_p$ associée.
• Application : grâce à cette relation, déterminer l’expression de l’énergie potentielle électrostatique $E_{pel}$ associée à la force électrostatique (cas d’un champ électrique uniforme) : $\overrightarrow{F_e}=qE\overrightarrow{u_y}$

Exercice de cours : le pendule simple, avec comme conditions initiales $\theta(0)=\theta_0$ et $\dot{\theta}(0)=0$ .
• Déterminer l’équation différentielle du mouvement en appliquant le P.F.D.
• En déduire l’intégrale première du mouvement.
(Evidemment, on fera un schéma, avec l’angle $\theta$ , la base polaire, et les vecteurs-forces).

Exercice de cours : le pendule simple, avec comme conditions initiales $\theta(0)=\theta_0$ et $\dot{\theta}(0)=0$ .
• Déterminer l’équation différentielle du mouvement en appliquant le T.E.C.
• Déterminer l’intégrale première du mouvement.
(Evidemment, on fera un schéma, avec l’angle $\theta$ , la base polaire, et les vecteurs-forces).

Exercice de cours : le pendule simple, avec comme conditions initiales $\theta(0)=\theta_0$ et $\dot{\theta}(0)=0$ .
• Déterminer l’équation différentielle du mouvement en appliquant le T.E.M.
• Déterminer l’intégrale première du mouvement.
(Evidemment, on fera un schéma, avec l’angle $\theta$ , la base polaire, et les vecteurs-forces).

Exercice de cours : le pendule simple, avec comme conditions initiales $\theta(0)=\theta_0$ et $\dot{\theta}(0)=0$ .
• Déterminer l’équation différentielle du mouvement en appliquant le T.M.C.
• Déterminer l’intégrale première du mouvement.
(Evidemment, on fera un schéma, avec l’angle $\theta$ , la base polaire, et les vecteurs-forces).

Soit un mouvement conservatif (c’est-à-dire ${\cal E}_M=cste$ ) à 1 degré de liberté (appelons-le par exemple $x$ , mais ça pourrait aussi être un angle $\theta$ …).

• Expliquer pourquoi l’énergie potentielle ne peut pas dépasser la valeur ${\cal E}_M$ de l’énergie mécanique.
• Comment qualifie-t-on un système qui est « coincé » dans une zone de l’espace ? A l’inverse, que dit-on quand il peut s’éloigner à l’infini ?

Soit un mouvement conservatif (c’est-à-dire ${\cal E}_M=cste$ ) à 1 degré de liberté (appelons-le par exemple $x$ , mais ça pourrait aussi être un angle $\theta$ …).

• Démontrer que les positions d’équilibre correspondent aux extremums du profil d’énergie potentielle ${\cal E}_p(x)$ .
• Démontrer que l’équilibre est stable quand l’énergie potentielle est minimale (et inversement, que l’équilibre est instable quand l’énergie potentielle est maximale).

Soit un mouvement conservatif (c’est-à-dire ${\cal E}_M=cste$ ) à 1 degré de liberté (appelons-le par exemple $x$ , mais ça pourrait aussi être un angle $\theta$ …).

Montrer que l’on peut approximer le mouvement au voisinage d’une position d’équilibre stable par un oscillateur harmonique, et déterminer la pulsation des petites oscillations au voisinage de cet équilibre (en fonction de la masse $m$ de la particule, et de $\frac{d^2{\cal E}_p}{dx^2}\rvert_{x=x_{eq}}$ ).

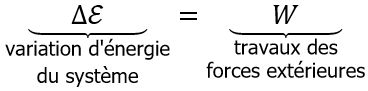
ASPECT ENERGETIQUE DE LA DYNAMIQUE

Puissance et travail d’une force.
– Reconnaître le caractère moteur ou résistant d’une force.
– Savoir que la puissance dépend du référentiel.
Loi de l’énergie cinétique et loi de la puissance cinétique dans un référentiel galiléen.
– Utiliser la loi appropriée en fonction du contexte.
Energie potentielle. Energie mécanique.
– Établir et connaître les expressions des énergies potentielles de pesanteur (champ uniforme), énergie potentielle gravitationnelle (champ créé par un astre ponctuel), énergie potentielle élastique, énergie électrostatique (champ uniforme et champ créé par une charge ponctuelle).
Mouvement conservatif.
– Distinguer force conservative et force non conservative. Reconnaître les cas de conservation de l’énergie mécanique. Utiliser les conditions initiales.
– Déduire d’un graphe d’énergie potentielle le comportement qualitatif : trajectoire bornée ou non, mouvement périodique, positions de vitesse nulle.
Positions d’équilibre. Stabilité.
– Déduire d’un graphe d’énergie potentielle l’existence de positions d’équilibre, et la nature stable ou instable de ces positions.
Petits mouvements au voisinage d’une position d’équilibre stable, approximation locale par un puits de potentiel harmonique.
– Identifier cette situation au modèle de l’oscillateur harmonique.
– Utiliser les résultats fournis par une méthode numérique pour mettre en évidence des effets non linéaires

THEOREME DU MOMENT CINETIQUE (EN MECANIQUE DU POINT !)

Moment cinétique d’un point matériel par rapport à un point et par rapport à un axe orienté
– Relier la direction et le sens du vecteur moment cinétique aux caractéristiques du mouvement.
– Maîtriser le caractère algébrique du moment cinétique scalaire.
Moment d’une force par rapport à un point ou un axe orienté
– Calculer le moment d’une force par rapport à un point ou à un axe orienté.
– Théorème du moment cinétique en point fixe dans un référentiel galiléen. Loi scalaire du moment cinétique dans un référentiel galiléen.
– Reconnaître les cas de conservation du moment cinétique.

Installer comme appli sur le téléphone