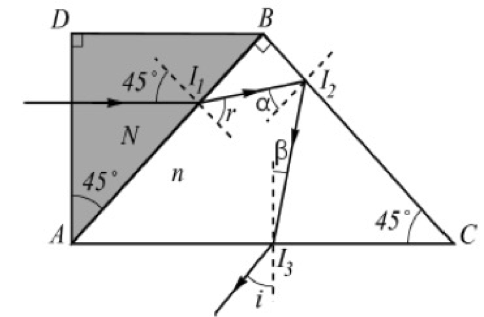
OPTIQUE – Prismes accolés – La Physique en PCSI

Deux morceaux de verre taillés sous forme de triangles rectangles et isocèles d’indices respectifs $N$ et $n$ ont leur face AB commune. Un rayon incident frappe AD sous une incidence normale, se réfracte en I₁, se réfléchit en I₂ puis ressort en I₃ sous l’incidence $i$ . Les valeurs de $N$ et $n$ sont telles que la réflexion soit totale en I₂.

1. Écrire la relation de Snell-Descartes aux points I₁ et I₃.

2. Quelles relations vérifient les angles $r$ et $\alpha$ ? $\alpha$ et $\beta$ ?

3. Quelle relation vérifient $N$ et $\alph$ pour que la réflexion soit totale limite en I₂ ? En déduire une relation entre $N$ et $n$ . Calculer $N$ , $r$ , $\alpha$ , $\beta$ et $i$ pour $n=1,5$ quand cette condition est réalisée. On appelle $N_0$ cette valeur limite de $N$ . Pour que la réflexion soit totale en I₂, $N$ doit-il être plus grand ou plus petit que $N_0$ ?

4. Écrire la relation vérifiée par $N$ et $n$ pour que l’angle $i$ soit nul. Que vaut alors $N$ ?