Du 11/03 au 15/03/2024 – La Physique en PCSI

Attention : trois chapitres au programme des colles cette semaine… n’attendez donc pas le dernier moment pour réviser ! 😉

physique des ondes ;
mouvement de particules chargées dans un champ 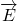$\overrightarrow{E}$ ou/et $\overrightarrow{B}$ ;
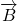le théorème du moment cinétique*.

*Remarque à destination des colleurs : le théorème du moment cinétique a été abordé en mécanique DU POINT uniquement, la mécanique du solide fera l’objet d’un chapitre ultérieur. Par ailleurs, la notion de bras de levier sera également traitée à ce moment-là, elle n’est donc pas exigible pour l’instant. (Comme d’habitude, la liste des compétences exigibles en colles cette semaine est rappelée dans le deuxième onglet ci-dessous.)

Certaines questions de cours portent également sur la fin du chapitre sur l’énergie (étude d’un petit mouvement au voisinage d’un équilibre stable, avec le développement limité autour de l’équilibre).

Questions de cours
Compétences exigibles en exercices

• Donner les deux écritures possibles d’une onde $s(x,t)$ se propageant le long d’un axe $(Ox)$ dans le sens des $x$ croissants, puis dans le sens des $x$ décroissants (propagation unidimensionnelle linéaire non dispersive).
• Même question, mais cette fois-ci pour une onde sinusoïdale.

• Concrètement, qu’appelle-t-on “différence de marche” $\delta$ entre deux ondes, en un point $P$ d’observation ?
• Quel est le lien entre la différence de marche $\delta$ , et le déphasage $\Delta\varphi$ entre deux ondes sinusoïdales ?
• Pour quelle(s) valeurs de $\delta$ a-t-on interférences constructives ? interférences destructives ?

On superpose deux signaux de même amplitude et de fréquences $f_1$ et $f_2$ légèrement différentes.
• Calculer le signal résultant, et tracer son allure en fonction du temps. Comment appelle-t-on ce phénomène ?
• Préciser la période des battements, et la fréquence du signal modulé par ces battements, en fonction des deux fréquences de départ $f_1$ et $f_2$ .

• Calculer l’onde résultant de la superposition de deux ondes sinusoïdales de même amplitude et de même pulsation, l’une se propageant dans le sens des $x$ croissants, l’autre dans le sens des $x$ décroissants.
• Pourquoi n’y a-t-il plus de phénomène de propagation ?
• Comment appelle-t-on une telle onde ?

Soit une onde stationnaire sinusoïdale sur une corde vibrante de longueur $L$ . La corde est fixée à ses deux extrémités (en $x=0$ et en $x=L$ ).

• Montrer par le calcul qu’il n’y a que certaines fréquences autorisées sur cette corde. Donner l’expression de ces fréquences, appelées “fréquences propres” (on notera $c$ la célérité des ondes mécaniques sur cette corde).
• Dessiner l’allure des quatre premiers modes de vibration de la corde, et vérifier que la relation entre la longueur d’onde et la longueur $L$ de la corde est bien cohérente avec les résultats trouvés précédemment.

On considère un mouvement conservatif à 1 degré de liberté $x$ .
• Justifier qu’une position d’équilibre correspond à un extremum d’énergie potentielle $E_p(x)$ .
• Puis justifier que cet équilibre est stable si cet extremum est un minimum.

• Montrer qu’il est possible d’approximer un mouvement au voisinage d’une position d’équilibre stable par un oscillateur harmonique.
• Déterminer alors la pulsation des petites oscillations autour de cet équilibre.

Expliquer pourquoi un champ magnétique peut dévier la trajectoire d’une particule chargée mais ne peut pas modifier la norme de sa vitesse (une démonstration est demandée).

Comment peut-on au laboratoire générer un champ électrique $\overrightarrow{E}$ uniforme ?
Préciser la norme $E$ du champ ainsi généré, en fonction des paramètres du montage.

Une particule chargée $q$ et de masse $m$ , initialement immobile en $A$ , est accélérée par une tension (différence de potentiel) $U=V_A-V_B$ appliquée entre deux plaques parallèles $A$ et $B$ . Par un bilan énergétique, déterminer sa vitesse atteinte en $B$ .

Déterminer le rayon de la trajectoire d’une particule chargée dans un champ magnétique uniforme dans le cas particulier où le vecteur-vitesse initial est perpendiculaire au champ magnétique, en admettant que cette trajectoire est circulaire.

– Définir le moment d’une force par rapport à un point $O$ , et par rapport à un axe $\Delta$ .
– Définir le moment cinétique d’un point matériel par rapport à un point $O$ , et par rapport à un axe $\Delta$ .

Énoncer puis démontrer le théorème du moment cinétique par rapport à un point $O$ .
(Ne pas oublier les hypothèses !…)

Exercice de cours : le pendule simple, avec comme conditions initiales $\theta(0)=\theta_0$ et $\dot{\theta}(0)=0$ .
• Déterminer l’équation différentielle du mouvement en appliquant le T.M.C.
• Déterminer l’intégrale première du mouvement.
(Evidemment, on fera un schéma, avec l’angle $\theta$ , la base polaire, et les vecteurs-forces).

PHYSIQUE DES ONDES

Exemples de signaux. Signal sinusoïdal.
Identifier les grandeurs physiques correspondant à des signaux acoustiques, électriques, électromagnétiques.

Approche qualitative de la superposition de deux signaux sinusoïdaux de fréquences voisines. Battements.

Propagation d’un signal dans un milieu illimité, non dispersif et transparent.
Onde progressive dans le cas d’une propagation unidimensionnelle non dispersive.
Célérité, retard temporel.
Ecrire les signaux sous la forme $f(x-ct)$ ou $g(x+ct)$ .
Écrire les signaux sous la forme $f(t-x/c)$ ou $g(t+x/c)$ .
Prévoir, dans le cas d’une onde progressive, l’évolution temporelle à position fixée et l’évolutions spatiale à différents instants.

Modèle de l’onde progressive sinusoïdale unidimensionnelle. Vitesse de phase, déphasage, double périodicité spatiale et temporelle.
Citer quelques ordres de grandeur de fréquences dans les domaines acoustique, mécanique et électromagnétique.
Établir la relation entre la fréquence, la longueur d’onde et la vitesse de phase.
Relier le déphasage entre les signaux perçus en deux points distincts au retard dû à la propagation

Milieux dispersifs et non dispersifs.
Définir un milieu dispersif (-> nous l’avons vu au tout début du chapitre A1, en début d’année !).
Citer des exemples de situations de propagation dispersive et non dispersive.

Interférences entre deux ondes acoustiques ou mécaniques de même fréquence.
Exprimer les conditions d’interférences constructives ou destructives.
Déterminer l’amplitude de l’onde résultante en un point en fonction du déphasage.

Interférences entre deux ondes lumineuses de même fréquence.
Exemple du dispositif des trous d’Young éclairé par une source monochromatique.
Différence de chemin optique. Conditions d’interférences constructives ou destructives. Formule de Fresnel.
Relier le déphasage entre les deux ondes à la différence de chemin optique.
Établir l’expression littérale de la différence de chemin optique entre les deux ondes.
Exploiter la formule de Fresnel fournie pour décrire la répartition d’intensité lumineuse.

Ondes stationnaires mécaniques. Modes propres.
Caractériser une onde stationnaire par l’existence de nœuds et de ventres.
Exprimer les fréquences des modes propres connaissant la célérité et la longueur de la corde.
Utiliser la propriété énonçant qu’une vibration quelconque d’une corde accrochée entre deux extrémités fixes se décompose en modes propres.
Relier les notions sur les ondes stationnaires avec celles utilisées en musique.

MOUVEMENT DE PARTICULES CHARGÉES DANS UN CHAMP ELECTRIQUE PUIS MAGNÉTIQUE UNIFORME ET PERMANENT

Force de Lorentz exercée sur une charge ponctuelle : champ électrique et magnétique
– Evaluer les ordres de grandeur des forces électrique ou magnétique et les comparer à ceux des forces gravitationnelles.

Puissance de la force de Lorentz
– Savoir qu’un champ électrique peut modifier l’énergie cinétique d’une particule alors qu’un champ magnétique peut courber la trajectoire sans fournir d’énergie à la particule.

Mouvement d’une particule chargée dans un champ électrostatique uniforme
– Mettre en équation le mouvement et le caractériser comme un mouvement à vecteur-accélération constant.
– Effectuer un bilan énergétique pour calculer la vitesse d’une particule chargée accélérée par une différence de potentiel.
– Citer une application.

Mouvement circulaire d’une particule chargée dans un champ magnétostatique uniforme dans le cas où le vecteur-vitesse initial est perpendiculaire au champ magnétique
– Déterminer le rayon de la trajectoire sans calcul en admettant que celle-ci est circulaire.
– Citer une application.

THEOREME DU MOMENT CINETIQUE (EN MECANIQUE DU POINT !)

Moment cinétique d’un point matériel par rapport à un point et par rapport à un axe orienté
– Relier la direction et le sens du vecteur moment cinétique aux caractéristiques du mouvement.
– Maîtriser le caractère algébrique du moment cinétique scalaire.
Moment d’une force par rapport à un point ou un axe orienté
– Calculer le moment d’une force par rapport à un point ou à un axe orienté.
– Théorème du moment cinétique en point fixe dans un référentiel galiléen. Loi scalaire du moment cinétique dans un référentiel galiléen.
– Reconnaître les cas de conservation du moment cinétique.

Installer comme appli sur le téléphone